Month: April 2021

A Peculiar Integral

Nassim Nicholas Taleb4 Comments

Prove

I= \displaystyle\int_{-\infty }^{\infty}\sum_{n=0}^{\infty } \frac{\left(-x^2\right)^n }{n!^{2 s}}\; \mathrm{d}x= \pi^{1-s}.

We can start as follows, by transforming it into a generalized hypergeometric function:

I=\displaystyle\int_{-\infty }^{\infty }\, _0F_{2 s-1} (\overbrace{1,1,1,...,1}^{2 s-1 \text{times}}; -x^2)\mathrm{d}x, since, from the series expansion of the generalized hypergeometric function, \, _pF_q\left(a_1,a_p;b_1,b_q;z\right)=\sum_{k=0}^{\infty } \frac{\prod_{j=1}^p \left(a_j\right)_k z^k}{\prod_{j=1}^q k! \left(b_j\right)_k}, where (.)_k is the Pochhammer symbol (a)_k=\frac{\Gamma (a+k)}{\Gamma (a)}.

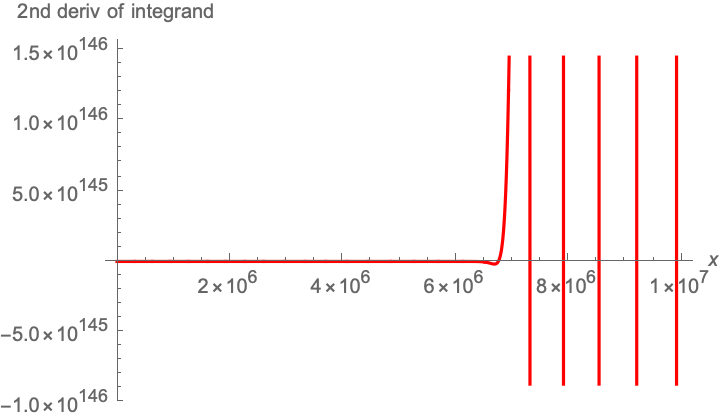
Now the integrand function does not appear to be convergent numerically, except for s= \frac{1}{2} where it becomes the Gaussian integral, and the case of s=1 where it becomes a Bessel function. For s=\frac{3}{2} and x=10^{19}, the integrand takes values of 10^{1015852872356} (serious). Beyond that the computer starts to produce smoke. Yet it eventually converges as there is a closed form solution. It is like saying that it works in theory but not in practice!

For, it turns out, under the restriction that 2 s\in \mathbb{Z}_{>\, 0}, we can use the following result:

\int_0^{\infty } t^{\alpha -1} _pF_q \left(a_1,\ldots ,a_p;b_1,\ldots ,b_q;-t\right) \, dt=\frac{\Gamma (\alpha ) \prod {k=1}^p \Gamma \left(a_k-\alpha \right)}{\left(\prod {k=1}^p \Gamma \left(a_k\right)\right) \prod {k=1}^q \Gamma \left(b_k-\alpha \right)}

Allora, we can substitute x=\sqrt(u), and with \alpha =\frac{1}{2},p=0,b_k=1,q=2 s-1, given that \Gamma(\frac{1}{2})=\sqrt(\pi),

I=\frac{\sqrt{\pi }}{\prod _{k=1}^{2 s-1} \sqrt{\pi }}=\pi ^{1-s}.

So either the integrand eventually converges, or I am doing something wrong, or both. Perhaps neither.

A Peculiar Integral