Introduction and Result
A maximum entropy alternative to Bayesian methods for the estimation of independent Bernouilli sums.
Let , where
be a vector representing an n sample of independent Bernouilli distributed random variables
. We are interested in the estimation of the probability p.
We propose that the probablity that provides the best statistical overview, (by reflecting the maximum ignorance point) is
, (1)
where and
is the beta regularized function.
Comparison to Alternative Methods
EMPIRICAL: The sample frequency corresponding to the “empirical” distribution , which clearly does not provide information for small samples.
BAYESIAN: The standard Bayesian approach is to start with, for prior, the parametrized Beta Distribution , which is not trivial: one is contrained by the fact that matching the mean and variance of the Beta distribution constrains the shape of the prior. Then it becomes convenient that the Beta, being a conjugate prior, updates into the same distribution with new parameters. Allora, with n samples and m realizations:
(2)
with mean . We will see below how a low variance beta has too much impact on the result.
Derivations
Let be the CDF of the binomial
. We are interested in
the maximum entropy probability. First let us figure out the target value q.
To get the maximum entropy probability, we need to maximize . This is a very standard result: taking the first derivative w.r. to q,
and since
is concave to q, we get
.
Now we must find p by inverting the CDF. Allora for the general case,
.
And note that as in the graph below (thanks to comments below by überstatistician Andrew Gelman), we can have a “confidence band” (sort of) with
;
in the graph below the band is for values of: .

Application: What can we say about a specific doctor or center’s error rate based on n observations?
Case (Real World): A thoraxic surgeon who does mostly cardiac and lung transplants (in addition to emergency bypass and aortic ruptures) operates in a business with around 5% perioperative mortality. So far in his new position in the U.S. he has done 60 surgeries with 0 mortality.
What can we reasonable say, statistically, about his error probability?
Note that there may be selection bias in his unit, which is no problem for our analysis: the probability we get is conditional on being selected to be operated on by that specific doctor in that specific unit.
Assuming independence, we are concerned with a binomially distributed r.v.
where n is the number of trials and
is the probability of failure per trial. Clearly, we have no idea what p and need to produce our best estimate conditional on, here,
.
Here applying (1) with and
, we have
.
Why is this preferable to a Bayesian approach when, say, n is moderately large?
A Bayesian would start with a prior expectation of, say .05, and update based on information. But it is highly arbitrary. Since the mean is , we can eliminate one parameter. Let us say we start with
and have no idea of the variance. As we can see in the graph below there are a lot of shapes to the possible distribution: it becomes all in the parametrization.

APPENDIX: JAYNES’ BRANDEIS PROBLEM
When I worked on this problem, and posted the initial derivations, I wasn’t aware of Jaynes’ “Brandeis Problem”. It is not the same as mine as it ignores n and it led to a dead-end because the multinomial is unwieldy. But his approach would have easily let to more work if we had computational abilities then (maximization, as one can see below, can be seamless).

Acknowledgments
Thanks to Saar Wilf for useful discussions.
Nassim:
It’s not clear you can come up with much of a “best estimate” from data with y=0. Maybe all that can be given in general (without using some prior information on p) are reasonable bounds. I like the Agresti-Coull procedure which gives a reasonable 95% interval. I’ve used this in a consulting project (in that case, the data were y=75 out of n=75) and put it in Regression and Other Stories.
LikeLiked by 1 person
Thanks, will update with a comment on bounds.
LikeLike
The problem of bounds requires a knowledge of . But there is such a thing as a maximum ignorance range, say between .25-.75. Replace
. But there is such a thing as a maximum ignorance range, say between .25-.75. Replace  by
by  and
and 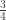 , and there is a band.
, and there is a band.
LikeLike
Excuse me, Maestro, but don’t you mean “where $m \geq \sum x_i$”, i.e. at most $m$ dead patients?
LikeLike
Wouldn’t make more sense to use $p_m = I^{-1}_{1/2}(m+1, n-m$? Same results, more coherent with the fact that you are inverting the CDF.
LikeLike