Background: We’ve discussed blood pressure recently with the error of mistaking the average ratio of systolic over diastolic for the ratio of the average of systolic over diastolic. I thought that a natural distribution would be the gamma and cousins, but, using the Framingham data, it turns out that the lognormal works better. For one-tailed distribution, we do not have a lot of choise in handling higher dimensional vectors. There is some literature on the multivariate gamma but it is neither computationally convenient nor a particular good fit.
Well, it turns out that the Lognormal has some powerful properties. I’ve shown in a paper (now a chapter in The Statistical Consequences of Fat Tails) that, under some parametrization (high variance), it can be nearly as “fat-tailed” as the Cauchy. And, under low variance, it can be as tame as the Gaussian. These academic disputes on whether the data is lognormally or power law distributed are totally useless. Here we realize that by using the method of dual distribution, explained below, we can handle matrices rather easily. Simply, if are jointly lognormally distributed with a covariance matrix
, then
are normally distributed with a matrix
. As to the transformation
, we will see the operation below.
Let be joint distributed lognormal variables with means
and a covariance matrix
allora follow a normal distribution with means
and covariance matrix
So we can fit one from the other. The pdf for the joint distribution for the lognormal variables becomes:
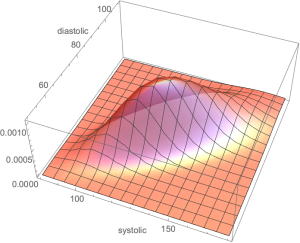
We have the data from the Framingham database for, using for the systolic and
for the diastolic, with
, which maps to:
.